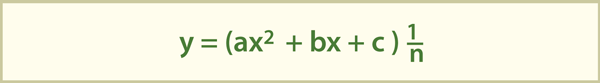Подготовка к ЕГЭ по математике с помощью Geogebra. Задача с параметром (С5)
Господа одиннадцатиклассники!
Скоро ЕГЭ по математике! Родители и учителя очень переживают! Можно понять! Мы ведь еще не привыкли к тому, что вы уже взрослые и на этом важном экзамене будете сами, совершенно самостоятельно, без всякого нашего участия принимать собственные решения. И, как показывает опыт прошлых лет, эти решения будут вполне на уровне. Совсем не хуже наших. А часто — лучше!
Но, с другой стороны, лично меня возмущает, когда уже сегодня иногда наблюдаются «сломанные крылья», истеричное уныние, опустившиеся руки, первобытные предрассудки и суеверия.
Ведь еще все, абсолютно все, в Ваших руках!
Ades animo et omitte timorem, — призывал когда-то Цицерон римлян, и Вам, без сомнения, следует тоже внять этому призыву «не падать духом и отбросить страх». Не бояться в математике — это значит думать самому, решать задачи самостоятельно. Научиться этому — как научиться плавать. Когда-то считалось, чтобы ребенок скорее поплыл, нужно столкнуть его неожиданно в воду. И обучая математике, многие учителя в прошлом рассуждали аналогично: задачку ему потруднее, и двойку, если не решит. В 21 веке так поступать уже не рационально. Оказалось, что научиться плавать можно без всякого шока, а для скорейшей успешности математического образования созданы мощные компьютерные средства. Надо только правильно ими пользоваться, не воспринимая их как шпаргалку.
Мы, например, с моими учениками в нашей гимназии используем на уроках математики Georebra. Эта компьютерная программа весьма известна и популярна в мировой педагогической практике. Рассказывать о ней можно долго, но лучше всего обратиться к первоисточнику (www.geogebra.org), который, возможно, как когда-то меня, увлечет вас, открыв новые горизонты наглядной, доступной всем математики.
Здесь же я хочу попробовать научить вас решать задачи типа С5 (задачи с параметром) второй части ЕГЭ с помощью этой программы.
ЗАДАЧА С5 С ПАРАМЕТРОМ
Итак, в прошлом году в одном из вариантов ЕГЭ давалась такая задачка С5:

Какие-то задачи с параметром Вы уже, конечно, решали. Например,

Все, конечно, понимают, что перед нами обыкновенное квадратное уравнение, второй коэффициент которого делится на 2.
Поэтому можно определить его дискриминант по упрощенной формуле. Дискриминант будет, очевидно, зависеть
от параметра а. Поэтому мы так его и обозначим: D(a).

Понятно, что данное квадратное уравнение имеет единственное решение тогда и только тогда, когда D(a) = 0. А это возможно при единственное значение параметра а равном 1. Это простенькое, даже и не задача, а, скорее, упражнение приведено как «мостик». Надо же с чего-то начинать решение нашей основной задачи.
Предположим, что такой же подход приведет и здесь нас к успеху. В самом деле: оставим в левой части радикал, все остальное перенесем в правую часть. Мы получим обыкновенное иррациональное уравнение. Возведем обе части в квадрат, выполним необходимые преобразование и, в конце концов, получим квадратное уравнение.
И здесь, наверное, тоже можно вывести D(a). Но угадывается уравнение от а четвертой степени,
в котором будут члены и третьей, и второй и первой. Может быть, конечно, что-нибудь и свернется.
Однако проверять это как-то не хочется! Что же делать? А если на экзамене такое?
Я советую решение задач с параметром начинать всегда с графических картинок.
Слева у нас парабола под радикалом. Что это такое графически пока непонятно — в школе мы этого не проходили.
Не ломая голову, обратимся к помощи Geogebra. Мгновенно получим такой график.
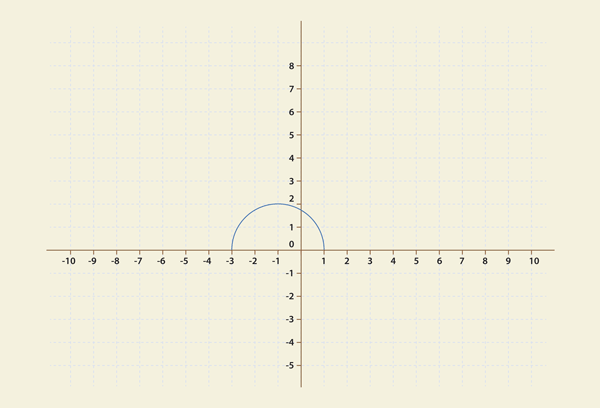
Очень похоже на параболу! Давайте сравним этот график с настоящей подрадикальной параболой. Вот что получится!

Что мы видим? Оказывается, параболоподобность нашего графика совсем не случайна! Почему? Оказывается «радикализм» т.е. функция у = √f(x) сохраняет промежутки возрастания и убывания основной, так сказать «несущей» функции f(x). А в данном случае абсцисса вершины параболы -1 и под радикалом останется абсциссой «горба». И «нули» те же: -3 и 1. Полностью «отрезана» нижняя отрицательная часть параболы и это понятно: нельзя извлекать квадратный корень из отрицательных значений.
Что дала нам эта картинка? Она научила нас, как схематично нарисовать без всякой Geogebra графики функций вида
Если сомневаетесь, нарисуйте самостоятельно несколько конкретных графиков этого типа, проверьте правильность
ваших построений с помощью моей апплеты «График подрадикальной функции» и вы убедитесь, что никакой компьютер
вам для такой работы уже не нужен.
Обратимся теперь к левой части уравнения: -ax-4a+2
Это, конечно, прямая, у которой и угловой коэффициент и свободный член зависит от а.
То есть, она двигается. Давайте с помощью Geogebra понаблюдаем за ее движением (апплета «Решение).
Что мы видим? Прямая очевидно вращается и, кажется, вокруг одной и той же точки.
Еще одно наблюдение: при больших а она приближается к вертикали х = - 4.
Решение задачи с помощью Geogebra (видео)
Апплета подсказывает нам и решение нашей задачи.
ПЕРВОЕ
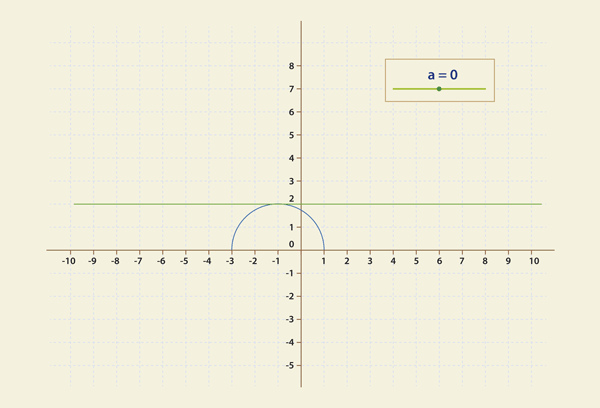
ВТОРОЕ
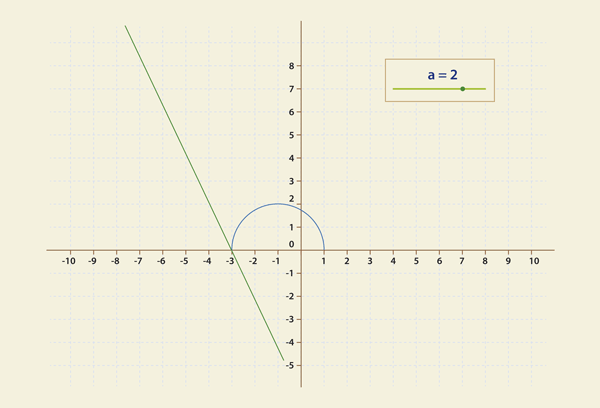
ТРЕТЬЕ: все положения прямой при
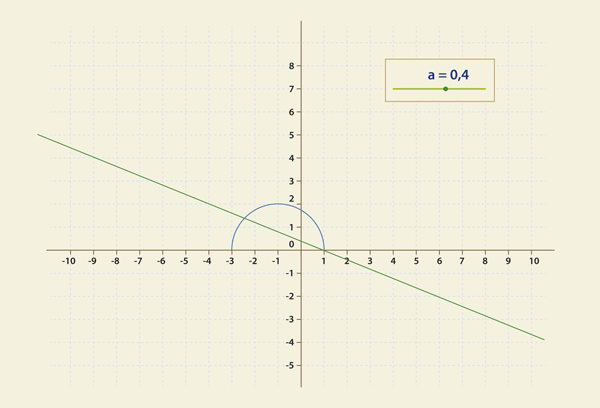
Итак, мы получили при помощи Geogebra опытные, эмпирические данные.
Теперь необходимо их понять, чтобы научиться решать такого рода задачи.
Ведь Geogebra не будет на экзамене.
Итак, почему прямая вращается?
Очевидно потому, что у нее изменяется угловой коэффициент.
Действительно ли она вращается вокруг одной точки? Давайте вычислим.
Пусть прямая с параметром а1 пересекается с прямой с параметром а2.
- а1х - 4а1 +2 = -а2х - 4а2 +2
- а1х + 4а1 = -а2х + 4а2
а2х - а1х = 4а1 - 4а2
(а2 - а1) х = 4 (а1 - а2)
х = - 4
Итак, все прямые пересекаются в точке с одной и той же абсциссой - 4
Подставив её в уравнений прямой, получим у = -а(-4) – 4а + 2 = 2.
Итак, все прямые пересекаются в одной и той же точке (-4, 2)
Найдем теперь предельное значение этой прямой.
у = -ах -4а + 2
у/а = -х -4 + 2/а
При больших а, левая часть и 2/а стремятся к нулю, т.е. предельное положение нашей прямой х = -4.
То есть, прямая не совсем вращается. При больших а, не важно положительных или отрицательных
она будет стремиться занять положение х = - 4 и, таким образом, график пересекать не сможет.
Теперь уже мы сами можем нарисовать окончательную картинку решения задачи.
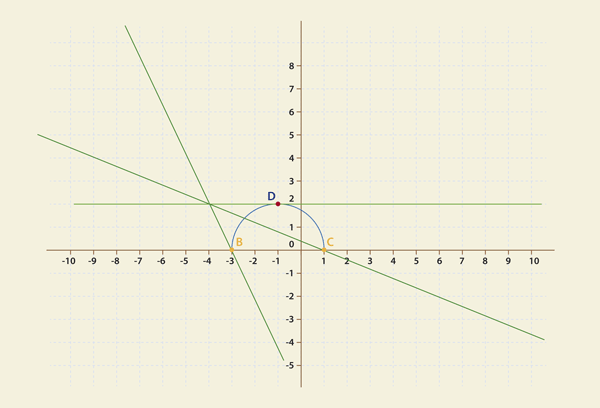
Отсюда ПЕРВОЕ РЕШЕНИЕ (касательная)
2 = -а(-1) -4а + 2а = 0
ВТОРОЕ РЕШЕНИЕ:
0 = - а(-3) -4а + 2, а = 2
ТРЕТЬЕ РЕШЕНИЕ: очевидно, что до пересечения прямой в абсциссе 1
она пересекает нашу пвевдопараболу только в одной точке.
Это пересечение происходит при значении а
0 = -а(1) -4а + 2 т.е. а = 0.4
В этой точке уже два решения. Значит
Итак, задача решена.
В заключение попробую сформулировать принцип целесообразности
использования Geogebra при подготовке к экзамену.
Часть «С» требует довольно серьёзной аналитической работы. Такая работа и в математике, и вообще в жизни
всегда сложна и, следовательно, чревата ошибками. Минимизировать их можно имея широкую опытную базу,
богатую эмпирику. Все это достигается тренировкой, но зачем же тратить месяцы, когда для того чтобы получить
данные для решения, например, этой задачи с помощью компьютера понадобилось не более 15 минут?