К двадцатипятилетию Классической гимназии при Греко-латинском кабинете Ю.А. Шичалина
Журнал Классической гимназии при Греко-латинском кабинете Ю.А. Шичалина. Выпуск 3
1997
Над этим выпуском журнала работали: Марина Георгиевна Алхазова — сбор материала и редактирование;
Виталий Егорович Сусленков — помощь в оформлении
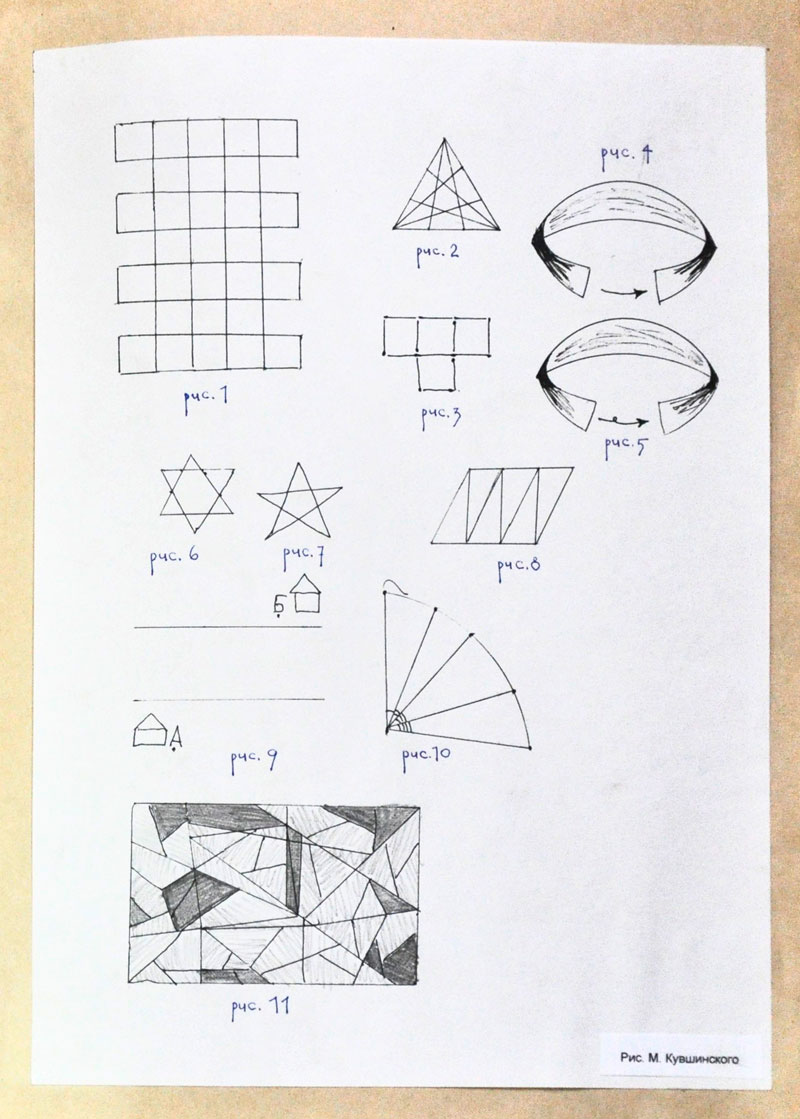
Сколько квадратов на рис. 1?
Сколько треугольников на рис. 2?
Как переложить 4 спички на фигуре — рис. 3, — чтобы получилось три прямоугольника?
Возьмите две полоски бумаги. Одну склейте, как показано на рис. 4, а другую так, как на рис. 3.
После этого закрасьте только одну сторону ленты и посмотрите на эти две ленты. Что в них удивительного?
Можно ли, не отрывая руки, нарисовать шестиконечную звезду? А пятиконечную? Рис. 6 — 7.
Сколько четырехугольников на рис. 8?
Можно ли квадрат, треугольник и круг вписать друг в друга так, чтобы у квадрата никакая сторона не была параллельна сторонам треугольника? Если так сделать можно, то нарисуйте, пожалуйста, что у Вас получилось.
Алеша живет в доме «А», и он захотел пойти в гости к Пете, который живет в доме «А» через реку. Какое путь будет самым коротким? В каком месте нужно переплыть реку, с условием, что плыть можно только перпендикулярно берегу реки? Рис. 9.
Сколько углов на рис. 10? С помощью транспортира измерьте их, а измерив, решите, какую часть круга они составляют?
Алеша захотел поехать к своему другу, живущему в сорока двух км. от его дома. До пруда он ехал сначала на поезде со скоростью 6 км/час, затем на автобусе со скоростью 4 км/час, а потом шел пешком со скоростью 2 км/час. А обратно он шел пешком, ехал в поезде и на автобусе. Задай разумные вопросы и ответь на них.
Найдите квадрат или квадраты на рис. 11.
Решите этот пример:
(((24 х 6 - (34 + 11 )) : 9 ) : ( 10 - ( 2 + 5 ) х 7 )) : 3


